Численное моделирование гистерезиса при обтекании осесимметричного сопла


Просмотр статьи
PDF, 1,3 МБ

Numerical Simulation of Hysteresis in Flow Around an Axisymmetric Nozzle

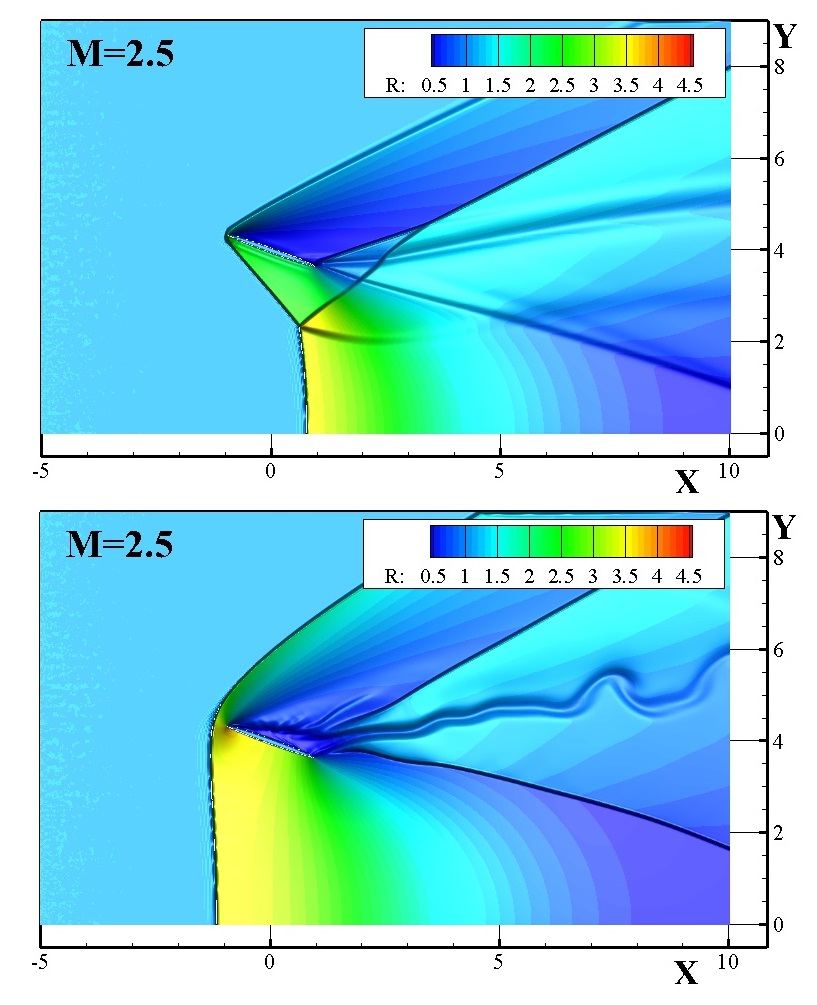
The paper presents the results of numerical simulation of axisymmetric flows near a converging nozzle by a supersonic flow of a perfect gas. A multi-block computational technology is applied using local curved grids adapted to the surface of bodies, which have finite overlap regions with a global rectangular grid for the entire computational domain. Viscous boundary layers are resolved on local grids using the Navier-Stokes equations, and the effects of aerodynamic interference of accompanying shock-wave structures are described within the framework of the Euler equations. In the areas of grid overlap, interpolation of functions is used up to the boundaries of the transition from one grid to another. With a sequential increase or decrease in the Mach number of the in-cident supersonic flow, a qualitative restructuring of the flow structure near the nozzle is detected - either a detached shock wave and a subsonic flow zone in front of the nozzle, or oblique shocks are formed. A hysteresis has been revealed, which is expressed in the fact that in a certain range of Mach numbers, the flow structure and aerodynamic load on the nozzle depend not only on the value, but also on the history of the change in the Mach number. Two flow variants in the flow hysteresis region at a Mach number of M = 2.5 are shown in the figure. The possibility of changing the flow structure by introducing density inhomogeneity into the incident flow is shown.

axisymmetric nozzle, shock-wave structures, aerodynamic characteristics, hysteresis, flow structure control.

DOI: http://doi.org/10.33257/PhChGD.26.1.1160


Том 26, выпуск 1, 2025 год



Представлены результаты численного моделирования осесимметричных сверхзвуковых ламинарных течений около сужающего сопла. Применена многоблочная вычислительная технология с использованием локальных адаптированных к поверх-ности тел криволинейных сеток, имеющих конечные области перекрытия с глобальной прямоугольной сеткой для всей расчетной области. Вязкие пограничные слои разрешаются на локальных сетках с использованием уравнений Навье ‒ Стокса, а эффекты аэродинамической интерференции сопутствующих ударно-волновых структур описываются в рамках уравнений Эйлера. В областях перекрытия сеток применяется интерполяция функций до границ перехода от одной сетки к другой. При последовательном увеличении или уменьшении числа Маха набегающего сверхзвукового потока обнаружена качественная перестройка структуры течения около сопла - образуются либо отошедшая ударная волна и дозвуковая зона течения перед соплом, либо косые скачки. Выявлен гистерезис, выражающийся в том, что в определенной области чисел Маха структура течения и аэродинамическая нагрузка на сопло зависят не только от величины, но и от предыстории изменения числа Маха. Показана возможность изменения структуры течения с помощью введения в набегающий поток неоднородности по плотности.

осесимметричное сопло, ударно-волновые структуры, аэродинамические характеристики, гистерезис, управление структурой течения.

DOI: http://doi.org/10.33257/PhChGD.26.1.1160


Том 26, выпуск 1, 2025 год



1. Зубин М.А., Туник Ю.В. Запуск сопла Лаваля в набегающем потоке. Известия Россий-ской академии наук. Механика жидкости и газа. 2014, №4, с. 155-160.
2. Максимов Ф.А., Шевелев Ю.Д. Моделирование обтекания проницаемых поверхностей. Математическое моделирование, 2018, №11, с. 127-144.
3. Максимов Ф.А., Чураков Д.А., Шевелев Ю.Д. Разработка математических моделей и численных методов для решения задач аэродинамического проектирования на много-процессорной технике. ЖВММФ, 2011, т.51, №2, с.303–328.
4. Максимов Ф.А. Численное моделирование гистерезиса при обтекании плоского сопла. Математическое моделирование и численные методы, 2023, №4, с.27-46.
5. Туник Ю.В. Запуск сопла Лаваля в набегающем потоке. Известия Российской академии наук. Механика жидкости и газа, 2011, №5, с. 120-127.
6. Иванов М.С., Кудрявцев А.Н., Хотяновский Д.В. Численное моделирование перехода между регулярным и маховским отражением ударных волн под воздействием локальных возмущений. Доклады Академии наук, 2000, т.373, №3, с. 332-336.
7. Алексеев А.К. Управление переходом между регулярным и маховским режимами взаи-модействия ударных волн. ЖВММФ, 2012, т.53, №6, с.1134–1142.
8. Алексеев А.К. О переходем между регулярным и маховским режимами взаимодействия ударных волн под воздействием возмущения температуры. Известия Российской акаде-мии наук. Механика жидкости и газа. 2012, №5, с.107-113.
9. Георгиевский П.Ю., Левин В.А. Управление обтеканием различных тел с помощью лока-лизованного подвода энергии в сверхзвуковой набегающий поток. Известия Российской академии наук. Механика жидкости и газа, 2003, №5, с. 154-167.
10. Schulein E., Zheltovodov A.A., Pimonov E.A, Loginov M.S. Study of the bow shock interac-tion with laser pulse heated air bubbles. AIAA Paper. 2009. №3568.
11. Fokeev V.P., Grin Yu.I., Levin V.A., Sharov Yu.L., Tunik Yu.V. The influence of gas dis-charge on propagation of triple shock mach configuration – numerical and experimental inves-tigations // Proc. 5th Intern. Workshop on Magneto_Plasma Aerodynamics in Aerospace Appli-cations / Ed. By V.A. Bityurin. Moscow: IVTAN, 2003. P. 234–240.
12. Niederhaus J.H.J., Greenough J.A., Oakley J.G., Ranjan D., Anderson M.H., Bonazza R.A. Computational parameter study for the three dimensional shock bubble interaction // J. Fluid Mech. 2008. V. 594. Р. 85–124.
13. Schulein E., Zheltovodov A.A., Pimonov E.A., Loginov M.S. Experimental and numerical modeling of the bow shock interaction with pulse heated air bubbles // Int. J. Aerospace Inno-vations. 2010. V. 2. №3. P. 165–188.
14. Picone J.M., Boris J.P. Vorticity generation by shock propagation through bubbles in a gas. // J. Fluid Mech. 1988. V. 189. P. 23–51.