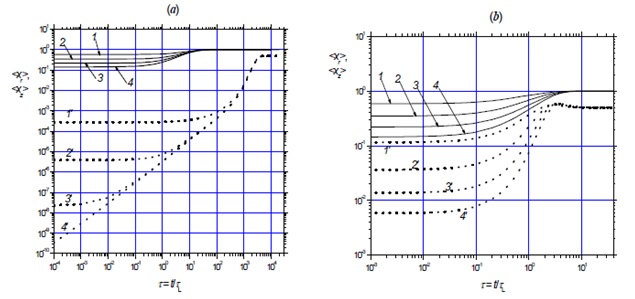
The kinetic equations describing the translational relaxation process in shock waves in extreme cases of the gas mixture: Rayleigh gas, i.e., a very dilute subsystem of heavy mass points dispersed in a heat bath of light particles, and Lorentz gas, i.e., a very dilute subsystem of light particles is dispersed in a heat bath of heavy particles, have been obtained. In contrast to existing ones, the equations take into account the fact that the problem of translational relaxation in the shock wave is not isotropic, namely, the direction of propagation of the shock wave is highlighted. The calculation results illustrate the radical difference between the process of translational relaxation in the flow behind the shock wave for the Lorentz and Rayleigh gases, which, in the latter case, has a substantially two-dimensional nature
Translational relaxation, gas mixture, shock wave, kinetic equations

Получены кинетические уравнения, описывающие процесс поступательной релаксации в ударных волнах в предельных случаях газовых смесей: газ Релея – малая примесь тяжелых частиц в термостате газа из частиц малой массы и газ Лоренца – малая примесь легких частиц в термостате тяжелых частиц. В отличие от существующих полученные уравнения учитывают то обстоятельство, что задача о поступательной релаксации в ударной волне не является изотропной, а именно: выделено направление распростране-ния ударной волны. Представлены результаты расчетов, иллюстрирующие радикальное различие процесса поступательной релаксации в потоке за фронтом ударной волны в га-зах Лоренца и Релея, который в последнем случае имеет существенно двумерный характер
Поступательная релаксация, газовая смесь, ударнаая волна, кинетические уравнения