О вращении сферического тела в вязкой суспензии


Просмотр статьи
PDF, 546,0 КБ

The Rotation of Spherical Body In Viscous Suspension

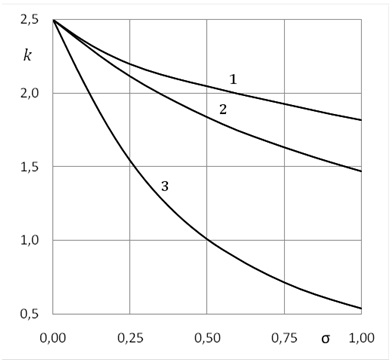
We consider the problem of the rotational motion of a spherical body in an unbounded viscous suspension in the Stokes approximation for the carrier continuous medium. An expression is obtained for the torque acting on the body in the first approximation in the volume fraction of the dispersed phase. Based on the solution obtained an expression is found for the effective viscosity of suspension, "as seen" by the body while rotating in a dispersed medium. It is shown that the coefficient for the volume fraction in the formula for the effective viscosity of suspension depends on the scale factor – the ratio of radius of dispersed particles and a body. Based on a comparison with the results of the previously discussed problems of the translational motion of a solid sphere and a spherical bubble in a viscous suspension it is shown that the effective viscosity of suspension depends also on the boundary conditions on the surface of the body and on the character of its motion in dispersed medium. In the particular case when the size of the dispersed particles is negligible compared to the size of the body, all the formulae obtained coincide with Einstein's result.

hydrodynamic interaction, dispersed medium, viscosity, suspension, self-consistent field method


Том 16, выпуск 2, 2015 год



Рассмотрена задача о вращательном движении сферического тела в безграничной вязкой суспензии в приближении Стокса для несущей сплошной среды. Получено выражение для момента сил, действующего на тело, в первом приближении по объемной концентрации дисперсной фазы. На основе полученного решения найдено выражение для эффективной вязкости суспензии, как ее «видит» тело при вращении в дисперсной среде. Показано, что коэффициент при объемной концентрации в формуле для эффективной вязкости суспензии зависит от масштабного фактора – отношения размеров дисперсных частиц и тела. На основе сравнения с результатами ранее рассмотренных задач о поступательном движении твердой сферы и сферического пузыря в вязкой суспензии показано, что эффективная вязкость суспензии зависит также от граничных условий на поверхности тела и характера его движения в дисперсной среде. В частном случае, когда размер дисперсных частиц пренебрежимо мал по сравнению с размером тела, все полученные формулы совпадают с результатом Эйнштейна.

гидродинамическое взаимодействие, дисперсная среда, вязкость, суспензия, метод самосогласованного поля


Том 16, выпуск 2, 2015 год



1. Cunningham E. On the velocity of steady fall of spherical particles through fluid medium // Proc. Roy. Soc. London. Ser. A. 1910. V. 83. P. 357–365.
2. Smoluchowski M.S. Uber die Wechselwirkung von Kugeln, die sich in einer zahen Flussigkeit bewegen // Bull. Int. Acad. Sci. Cracovie. Ser. 1A. 1911. P. 28–39.
3. Струминский В.В., Гуськов О.Б., Кульбицкий Ю.Н. Гидродинамика дисперсных и газожидкостных потоков // Докл. АН СССР. 1984. Т. 278. № 1. С.65–68.
4. Гуськов О.Б., Струминский В.В. Динамика дисперсных потоков в присутствии границ // Докл. АН СССР. 1985. Т. 285. № 4. С. 832–835.
5. Гуськов О.Б., Золотов А.В. Об осаждении суспензии сферических частиц в цилиндре // ПММ. 1987. Т. 51. Вып. 6. С. 968–972.
6. Гуськов О.Б. О взаимодействии частиц в вязкой жидкости в присутствии границ // В сб.: Гидродинамические проблемы технологических процессов. – М.: Наука, 1988. С. 71–77.
7. Струминский В.В., Гуськов О.Б., Корольков Г.А. Гидродинамическое взаимодействие частиц в потенциальных потоках идеальной жидкости // Докл. АН СССР. 1986. Т. 290. № 4. С. 820–824.
8. Гуськов О.Б., Бошенятов Б.В. Гидродинамическое взаимодействие сферических частиц в потоке невязкой жидкости // Докл. Акад. Наук. 2011. Т. 438. № 5. С. 626–628.
9. Гуськов О.Б. О присоединенной массе тела, движущегося в суспензии сферических частиц // Докл. Акад. Наук. 2012. Т. 442. № 1. С. 50–53.
10. Гуськов О.Б. Присоединенная масса сферы в суспензии сферических частиц // ПММ. 2012. Т. 76. Вып. 1. С. 134–139.
11. Бошенятов Б.В. Гидродинамическое взаимодействие и присоединенная масса дисперсных частиц // Известия ВУЗ. Физика. 2014. Т. 57. № 8/2. С. 50–60.
12. Бошенятов Б.В. К теории электро- и теплопроводности пузырьковых газожидкостных сред // Докл. Акад. Наук. 2014. Т. 459. № 6. С. 693–695.
13. Бошенятов Б.В. К расчету эффективных коэффициентов переноса в монодисперсных суспензиях сферических частиц // Письма в ЖТФ. 2015. Т. 41. Вып. 3. С. 67 – 73.
14. Гуськов О.Б. Метод самосогласованного поля применительно к динамике вязких суспензий // ПММ. 2013. Т. 77. Вып. 4. С. 557–572.
15. Schmitz R., Felderhof B.U. Creeping flow about a sphere // Physica A. 1978. V. 92. Issues 3–4. P. 423–437.
16. Batchelor G.K. Sedimentation in a dilute dispersion of spheres // J. Fluid Mech. 1972. V. 52. Pt. 2. P. 245–268.
17. Beenakker C.W.J., Mazur P. Is sedimentation container-shape dependent? // Phys. Fluids. 1985. V. 28. No. 11. P. 3203–3206.
18. Гуськов О.Б. О движении сферического тела в вязкой суспензии // Докл. Акад. Наук. 2014. Т. 456. № 4. С. 420–423.
19. Einstein A. Eine neue Bestimmung der Molekiildimensionen // Ann. Physik. 1906. V. 19. P. 289–306.
20. Гуськов О.Б. К вопросу об эффективной вязкости разбавленной суспензии твердых сферических частиц // ПММ. 2015. Т. 79. Вып. 5. С. 644–652.
21. Happel J.R., Brenner H. Low Reynolds number hydrodynamics. – Springer. 1965. 533 p.